Аппроксимация прогнозируемых величин. Сглаженный шаблон максимальной прибыли
Рассмотрим перцептрон с одним выходным нейроном. Подавая на входы этого перцептрона любые числа x1, x2, ..., xn, получим на выходе значение некоторой функции F(x1, x2, ..., xn), которое является ответом (реакцией) сети. Очевидно, что ответ сети зависит как от входного сигнала, так и от значений ее внутренних параметров - весов нейронов.
Естествен вопрос: а может ли перцептрон реализовать достаточно сложную функцию? Этот вопрос, по своей сущности, математический - о представимости одних функций посредством других. Ученые занимались решением этой задачи долгое время и ответ был получен сравнительно недавно - в 1989 г. В результате продолжительных исследований несколькими учеными практически одновременно была сформулирована теорема, которая на языке нейросетей звучит так: «Любую непрерывную функцию нескольких переменных можно с любой точностью реализовать с помощью обычного трехслойного перцептрона с достаточным количеством нейронов в скрытом слое». Это означает, что с помощью стандартного перцептрона в принципе возможно решать любые задачи прогнозирования и оценки, в которых существуют функциональные зависимости. Здесь указывается «в принципе», так как теорема не указывает, каким способом можно подобрать веса каждого нейрона, используя набор примеров.
Если на рынке существуют функциональные зависимости, то успех решения задачи аппроксимации, кроме всего прочего, во многом будет зависеть от выбора прогнозируемой величины - обучающего правила. Рассмотрим пример формирования величины, достоверный прогноз которой позволял бы получать максимальную прибыль при торговле на рынке.
Как показано выше, в качестве обучающего правила можно взять MPP. Однако, MPP в чистом виде содержит дискретные данные, что делает задачу достаточно сложной. Кроме того, как показывает практика, для ведения оптимальной торговли, большую часть времени на рынке приходится ожидать возможности «войти в рынок». Построенная для такого рынка MPP будет содержать большое количество сигналов на «ожидание» покупки или продажи.
При обучении по такому правилу ИНС начнет «тяготеть» к формированию на выходе тех сигналов, которые чаще встречаются в обучающем множестве. Рассмотрим ряд MPP, построенный для динамики курса евро/доллар за 1999 год (см. рис. 2.11).

Рис. 2.11. Распределение желаемых выходных значений ИНС при применении в качестве обучающего правила «необработанного» MPP
Как показывает опыт, при прогнозировании по графическим образам добиться от сети точных данных на выходе невозможно, попытаемся облегчить для сети задачу обучения, а именно, сгладим значения MPP 6-типериодной скользящей средней. Гистограмма распределения выходного сигнала, таким образом, примет вид, изображенный на рисунке 2.12. Фактически график значений обучающего правила примет вид, изображенный на рисунке 2.9 (красная линия).
Особо хочется отметить тот факт, что обучающее множество желательно формировать таким образом, чтобы распределение выходных сигналов тяготело к равномерному, как показывает практика. Это позволит существенно уменьшить среднеквадратическую ошибку ИНС. В нашем случае (рис. 2.12), не смотря на некоторое приближение распределения сглаженного MPP к равномерному, распределение полученной после преобразования величины далеко до равномерного.
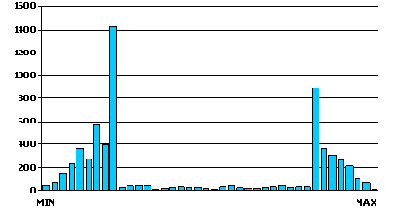
Рис. 2.12. Распределение значений на выходе последнего нейрона ИНС при применении в качестве обучающего правила сглаженного (6-типериодной скользящей средней) MPP (база - евро/доллар 1999)
Кроме того, в течении 1999 года евро больше падала в цене, следовательно сигналов на продажу и ожидание продажи в обучающей выборке получится больше, чем сигналов на покупку и ожидание покупки. Сразу можно говорить о том, что обученные по такому правилу ИНС будут «тяготеть» к сигналу «ожидание продажи». Необходимо использовать алгоритм формирования обучающей выборки, который бы позволял избегать излишнего доминирования отдельных выходных значений.
Возможными прогнозируемыми величинами при реализации задачи прогнозирования могут являться: доходность и ценовые показатели, то есть средневзвешенная цена, цены закрытия и открытия, максимальная и минимальная цены.Причем прогнозироваться могут как показатели, определенные для целой группы инструментов или некоторого рынка в целом, так и показатели, определенные только для одного инструмента финансового рынка. В некоторых пакетах нейросетевого анализа финансовых рынков встроены модели, позволяющие прогнозировать максимальные и минимальные значения цены на один или несколько шагов вперед.
